消光比不同的光柵，各級衍射光的效率
超分辨成像過程中，會(hui) 在LCOS上加載光柵圖形，產(chan) 生衍射光，利用正負一級光衍射產(chan) 生需要的圖案。但是有可能因為(wei) 光路問題，可能
導致成像光柵消光比有限，成像的消光比會(hui) 影響衍射光的效率，下麵介紹的是關(guan) 於(yu) ，不同消光比的情況下，零級光和其他級次的衍射光
的效率。
在Mathematica中，UnitBox表示一個(ge) 高度為(wei) 1，寬度有限的區域，我打算用這個(ge) 函數模擬光柵
Plot[UnitBox[2 x] + UnitBox[2 x - 2], {x, -3, 3}, Exclusions -> None]
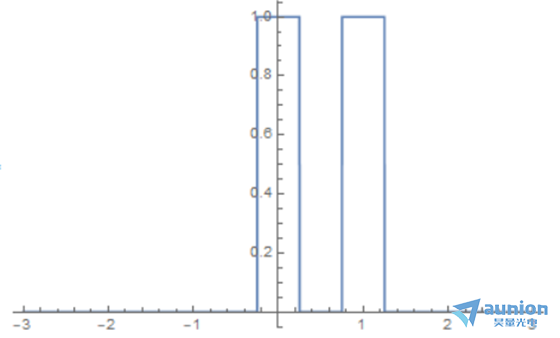
光柵的周期比較多，是對上述矩陣的複製和平移，可以使用DirectDelta函數即狄拉克函數和上述函數的卷積，來表示想要的結果，如
下所示。將下述的M從(cong) -3到3擴展到-n到n，就可能比較接近常用的光柵
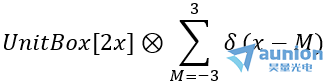
=UnitBox[2-2u]+UnitBox[4-2u]+UnitBox[6-2u]+UnitBox[8-2u])
Plot[UnitBox[2 - 2 u] + UnitBox[4 - 2 u] + UnitBox[6 - 2 u] +
UnitBox[2 u] + UnitBox[2 (1 + u)] + UnitBox[2 (2 + u)] +
UnitBox[2 (3 + u)], {u, -5, 5}, Exclusions -> None]
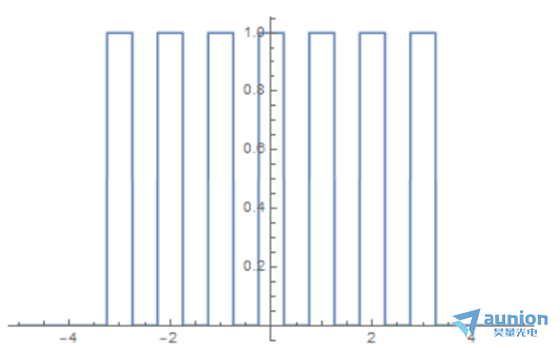
將上述M取值範圍修改為(wei) -n到n之間
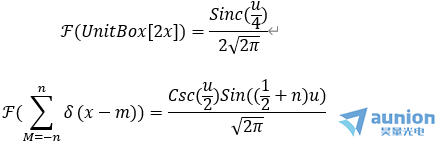
那麽(me) 最終光強公式可以表示為(wei)
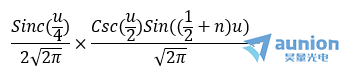
當n=1024時
Plot[((Csc[u/2] Sin[(2049 u)/2] Sinc[u/4])/(4 \[Pi]))^2, {u, -2 \[Pi] - 1, 2 \[Pi] + 1}, PlotRange -> All]
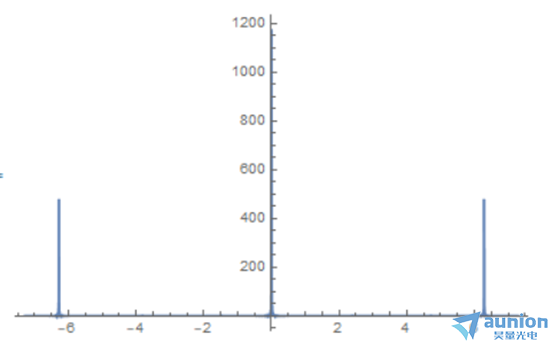
若降低對比度，那麽(me) 起初的UnitBox可以改寫(xie) 為(wei) 如下格式
Plot[UnitBox[2 x]*0.8 + 0.1, {x, -1, 1}]
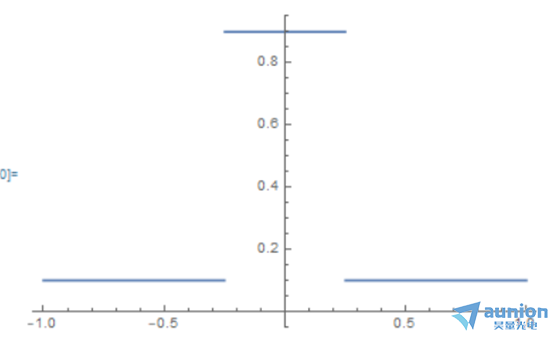
對新的UnitBox重新進行傅裏葉變化，其中m描述的是對比度的參數
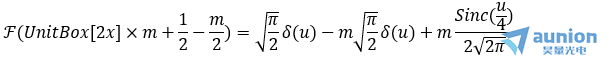
我處理狄拉克函數是，僅(jin) 當函數內(nei) 部為(wei) 零時值為(wei) 1，其他情況為(wei) 0
因此零級光強為(wei)
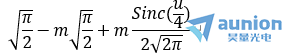
一級光強為(wei)
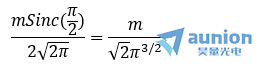
二級光強為(wei)
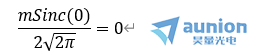
三級光強為(wei)
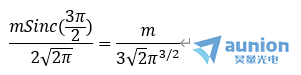
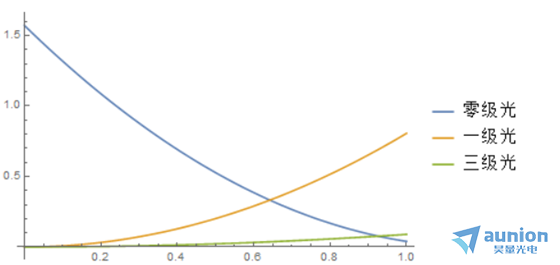
因為(wei) 二級光強永遠為(wei) 零，觀察零級光，一級光，三級光相對於(yu) 對比度的變化，因為(wei) 一級光和三級光的光強太弱，因此乘以係數50
Plot[{(Sqrt[\[Pi]/2] - m Sqrt[\[Pi]/2] + m /(2 Sqrt[2 \[Pi]]))^2, ( m/(Sqrt[2] \[Pi]^(3/2)))^2*50, (-(m/(3 Sqrt[2] \
[Pi]^(3/2))))^2*50}, {m, 0, 1},
PlotLegends -> {"零級光", "一級光", "三級光"}]
實驗
在LCOS上加載間距相同的光柵，如下圖所示
下圖為(wei) 實際看到的效果，最亮的兩(liang) 點為(wei) 一級光，中間為(wei) 零級光，二級光的位置沒有光斑。
展示全部 
展示全部
